WOB Tutorial 3

Tracing Branches

As seen in Tutorial 2, solutions of parameterized equations form continua, which are called branches. The decisive solutions where something ``happens'' are bifurcations. At these points, the stability may be lost, or the structure of the state may change drastically. Bifurcations have a qualitative flavor whereas the branches represent quantitative elements. A particular example may have a few bifurcation points, but it has an infinite number of solutions, at least one for each parameter value. Accordingly, the bulk of computations is the computation of the branches. The effort devoted to bifurcations is a relatively small fraction of the total expenses. Branches and bifurcations must be computed both. The resulting bifurcation diagram is the signature of the problem. This Tutorial 3 is devoted to the computation of the branches. The calculation of bifurcations is discussed in Tutorial 4. We shall concentrate on basic principles.

Fig. 1. Left: a theoretical bifurcation diagram;
right: a result of a numerical path following.

1. Predictor-corrector approach

The procedure will be studied on the formally simple problem

$\begin{displaymath}{\bf f}({\bf y},\lambda)=\00.\eqno{(1)}\end{displaymath}$

Only a finite selection of the infinitely many (solution,parameter)-combinations $({\bf y},\lambda)$ can be calculated--that is, we do not obtain the curves in the branching diagrams but approximate discrete points on the curve. The process of tracing a branch by calculating representative solutions $({\bf y}^j,\lambda_j)$ on that branch for $j=0,1,2,\ldots$ with certain distances apart is called continuation, or path following (Figure 1). The calculated chain of points, in turn, may be interpolated by some smooth curve, which then approximates the branch. We now discuss a single step of a continuation method, namely the transition from a calculated solution $({\bf y}^j,\lambda_j)$ to the next solution with number j+1,

$\begin{displaymath}({\bf y}^j, \lambda_j) \to ({\bf y}^{j+1}, \lambda_{j+1}).\end{displaymath}$

This detail is illustrated by Figure 2, which summaries the predictor-corrector approach. With predictor-corrector methods, the step $j\to j+1$ is split into two steps:

$\begin{displaymath}({\bf y}^j ,\lambda_j) \vbox{\baselineskip=2pt \hbox{ \ pre... ...x to2{ \rightarrowfill }} ({\bf y}^{j+1},\lambda_{j+1}).\end{displaymath}$

In general, the predictor $(\bar {\bf y}, \bar \lambda)$ is not a solution of Eq.(1). The predictor merely provides an initial guess for corrector iterations that home in on a solution of Eq.(1). In Figure 2 the corrector iteration is indicated by dots. The major portion of the work is either on the predictor step (resulting in an approximation $(\bar {\bf y}, \bar \lambda)$ close to the branch) or on the corrector step (if a ``cheaper" predictor has produced a guess far from the branch). The distance between two consecutively calculated solutions $({\bf y}^j,\lambda_j)$ and $({\bf y}^{j+1},\lambda_{j+1}$ ) is called the step length or step size. This distance can be measured approximately, for example, by the length of the predictor step. In addition to Eq.(1), we need a parameterization strategy that identifies the location of a solution on the branch. In summary, the basic ingredients of predictor-corrector methods are:

( $\alpha$ ) predictor, ( $\beta$ ) parameterization strategy, ( $\gamma$ ) corrector, and ( $\delta$ ) step-length control.

The first three of these four items can be chosen independently of each other. But the step-length control must match the predictor, the corrector, and the underlying parameterization. All of the four ingredients have a local nature -- that is, they should be valid for the step $j\to j+1$ and may be changed for the next step.

Fig. 2. Predictor-corrector principle.

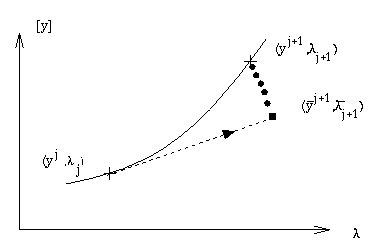
2. Predictors

Here we outline how the branch is locally approximated by a straight line. Taking the differential of both sides of Eq.(1), one obtains

$\begin{displaymath}\00 = d{\bf f}={\bf f}_{\bf y}d{\bf y}+ {\bf f}_\lambda d\lambda. \eqno(2)\end{displaymath}$

With the notation z_i = ith component of ${\bf z}$ , and setting

$\begin{displaymath}z_i = dy_i \ \ (1 \le i \le n) , \quad z_{n+1} = d\lambda,\end{displaymath}$

Eq.(2) is written

$\begin{displaymath}({\bf f}_{\bf y}\vert {\bf f}_\lambda ) {\bf z}= \00 \ .\eqno(3)\end{displaymath}$

Hence ${\bf z}\in\hbox{I}\hbox to 5.5pt{\hss R}^{n+1}$ is tangent to the branch. Equation (3) guarantees a unique straight line tangent to the branch in $({\bf y},\lambda)$ as long as the full-rank condition

$\begin{displaymath}\hbox{rank}({\bf f}_{\bf y}\vert {\bf f}_\lambda)=n \eqno(4)\end{displaymath}$

is satisfied. The length and the orientation of a vector ${\bf z}$ on this tangent are still undetermined. A normalization of ${\bf z}$ must be imposed to give Eq.(3) a unique solution. One can use as a normalizing equation ${\bf c}\hbox{{$^t$ }\hbox to 3.0pt{\hss $^r$ }}{\bf z}=1$ with, for example, ${\bf c}\! :={\bf e}_k$ . This leads to ${\bf e}^{\everymath{\scriptstyle}\everydisplay{\scriptstyle} \hbox{{$t$ }\hbox ... ...{\hss $r$ }} \everymath{\textstyle}\everydisplay{\textstyle}}_k{\bf z}= z_k =1,$ where ${\bf e}_k$ is the (n+1)-dimensional unit vector with all elements equal to zero except the kth, which equals unity ( $\hbox{{$^t$ }\hbox to 3.0pt{\hss $^r$ }}$ denotes transpose). Then the tangent ${\bf z}$ is the solution of the linear system

$\begin{displaymath}\left({{\bf f}_{\bf y}\vert {\bf f}_\lambda \over {\bf e}_k^... ...rydisplay{\textstyle}}}\right){\bf z}={\bf e}_{n+1} . \eqno (5)\end{displaymath}$

Provided the full-rank condition (4) holds along the whole branch, Eq.(5) has a unique solution at any point on the branch (k may have to be changed). In particular, the tangent can be calculated at turning points.

Several continuation methods are based on tangent predictors. In these methods the predictor point (initial approximation) for $({\bf y}^{j+1} ,\lambda_{j+1})$ is

$\begin{displaymath}(\bar {\bf y}^{j+1}, \bar \lambda_{j+1}) : = ({\bf y}^j ,\lambda_j ) +\sigma_j{\bf z}\end{displaymath}$

(see Figure 2). Here $\sigma_j$ is an appropriate step length. This tangent predictor can be considered a step of the Euler method for solving a differential equation that describes the branch. Hence, the tangent predictor is of first order.

An alternative to the tangent is the secant

$\begin{displaymath}(\bar {\bf y}^{j+1} ,\bar \lambda_{j+1}): = ({\bf y}^j ,\lamb... ...sigma_j ({\bf y}^j -{\bf y}^{j-1} , \lambda_j -\lambda_{j-1}) \end{displaymath}$

(see Figure 3). The discretization error of the secant predictor is of the same order as the tangent predictor. Initially, no ``old" solution with index j-1 may be known. Then the secant is not defined, and one starts with the trivial predictor

$\begin{displaymath}(\bar {\bf y}^{j+1},\bar \lambda_{j+1}):=({\bf y}^j,\lambda_j)\, , \end{displaymath}$

which is the previous solution.

Fig. 3. Secant predictor.

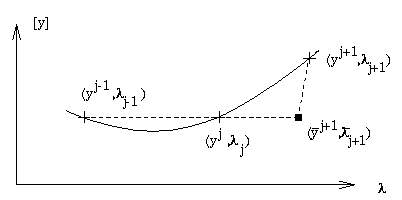
3. Parameterizations

The next step is to introduce a local measure along the branch. That is, the current part of the curve is ``parameterized." Terms like ``next" or ``previous" solution are quantified by introducing a parameterization. The most obvious parameter is the control variable $\lambda$ . While this parameter has the advantage of having physical significance, it encounters difficulties at turning points, where the tangent is normal to the parameter axis.

Curves such as solution branches of Eq.(1) can be parameterized by curve parameters. A general curve parameter, call it $\gamma$ , may have a geometrical rather than a physical meaning. A parameterization by $\gamma$ means that solutions of ${\bf f}({\bf y},\lambda )=\00$ depend at least locally on $\gamma$ : ${\bf y}={\bf y}(\gamma ),\ \lambda =\lambda (\gamma ).$ For a particular value of $\gamma$ , the system ${\bf f}({\bf y},\lambda )=\00$ consists of n equations for the n+1 unknowns $({\bf y},\lambda)$ . If the parameterization is established by one additional scalar equation, $p({\bf y},\lambda ,\gamma )=0$ , one can formulate an extended system

$\begin{displaymath}{\bf F}({\bf Y},\gamma):= \pmatrix {{\bf f}({\bf y},\lambda)\cr p({\bf y},\lambda,\gamma)\cr}=\00,\eqno (6)\end{displaymath}$

which consists of n+1 scalar equations for the n+1 unknowns ${\bf Y}=({\bf y},\lambda ).$ The general setting Eq.(6) includes all types of parameterization. For example, the option of taking $\lambda$ as continuation parameter means choosing $\gamma =\lambda$ and for a prescribed value of $\lambda_{j+1}$

$\begin{displaymath}p({\bf y},\lambda ) = \lambda -\lambda_{j+1}.\end{displaymath}$

Other examples will follow soon. Solving Eq.(6) for specified values of $\gamma$ yields information on the dependence ${\bf y}(\gamma ), \lambda (\gamma ).$

The parameterizing equation $p({\bf y},\lambda ,\gamma )=0$ is attached to the given system of Eq.(1). The resulting system (6) is a general equation on which general software of numerical analysis is applicable. We call the chosen software SOLVER; in our setting this may be Newton's method. In this way, by calling SOLVER for Eq.(6), the desired parameterization is imposed on Eq.(1) automatically. Alternatively, one can apply the Newton method to Eq.(1) and impose an appropriate side condition on the iteration. This latter approach will be described in Section 4. The formulation in Eq.(6) has the advantage of not being tied to a special version of a Newton method. Any modification or other iteration method for solving equations can be applied to solve Eq.(6).

A classical example of a curve parameter is the arclength s--that is, $\gamma =s.$ The arclength s has a global meaning. It satisfies both the linear system

$\begin{displaymath}0={\bf f}_{\bf y}{d {\bf y}\over d s}+{\bf f}_\lambda {d \lambda \over ds} \end{displaymath}$

(derived from Eq.(2)), and the nonlinear relation

$\begin{displaymath}(dy_1 /ds)^2 + \ldots + (dy_n /ds)^2 + (d\lambda /ds)^2 = 1.\end{displaymath}$

Both these equations form an implicit system of n+1differential equations for the n+1 unknowns

$\begin{displaymath}dy_1 /ds ,\ldots , dy_n /ds , \, d\lambda /ds.\end{displaymath}$

A corresponding equation $p({\bf y},\lambda ,s)=0$ is obtained by multiplying the arclength equation by (ds)². The resulting discretized parameterizing equation is

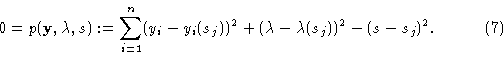
$\begin{displaymath}0 = p ({\bf y},\lambda ,s) :=\sum^n_{i=1}(y_i -y_i (s_j ))^2+(\lambda -\lambda(s_j))^2 - (s-s_j )^2.\eqno (7)\end{displaymath}$

If ${\bf Y}^j=({\bf y}^j ,\lambda_j )=({\bf y}(s_j ),\lambda (s_j ))$ is the solution previously calculated during continuation, Eq.(7) together with Eq.(1) fix the solution $({\bf y}(s),\lambda (s))$ at discretized arclength distance $\Delta s=s-s_j$ . The scalar Eq.(7) is nonlinear. ``Pseudo arclength" linearizes Eq.(7) making use of ${\bf y}(s)-{\bf y}(s_j)\approx (s-s_j)d{\bf y}(s_j)/ds$ . The resulting expression is linear in the increments $\Delta {\bf y}$ , $\Delta\lambda$ , $\Delta s$ ,

$\begin{displaymath}p({\bf Y},s):={\bf z}\hbox{{$^t$}\hbox to 3.0pt{\hss $^r$}}({\bf Y}-{\bf Y}^j)-(s-s^j)=0\, ,\eqno(8)\end{displaymath}$

and defines a plane normal to the tangent ${\bf z}$ .

Another important way to parameterize a branch is to admit any of the components y_i $(i=1,\ldots,n)$ as a parameter, including $y_{n+1}=\lambda$ . This local parameterization leads to the parameterizing equation

$\begin{displaymath}p({\bf y},\eta ): = y_k -\eta ,\eqno(9)\end{displaymath}$

with an index k, $1\le k\le n+1$ , and a suitable value of $\eta$ . The index k and the parameter $\eta=y_k$ are locally determined at each continuation step $({\bf y}^j,\lambda_j)$ in order to keep the continuation flexible. An index k for local parameterization exists whenever the full-rank condition Eq.(4) holds. Thus the turning around turning points is straightforward. With ${\bf Y}=({\bf y},\lambda )$ , Eq.(6) is written as

$\begin{displaymath}{\bf F}({\bf Y},\eta ,k) = \pmatrix {{\bf f}({\bf Y}) \cr y_k - \eta \cr} =\00. \eqno (10)\end{displaymath}$

It is easy to find a suitable index k and parameter value $\eta$ . A continuation algorithm based on tangent predictors determines k such that

$\begin{displaymath}\vert z_k \vert =\max \{\vert z_1\vert, \ldots,\vert z_n\vert, \vert z_{n+1}\vert \}. \end{displaymath}$

This choice picks the component of the tangent ${\bf z}$ that is maximal. For a secant predictor, index k is chosen such that $\Delta_r y_k$ is the maximum of all relative changes,

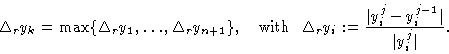
$\begin{displaymath}\Delta_r y_k = \max \{ \Delta_r y_1,\ldots, \Delta_r y_{n+1}\... ... y_i: = {\vert y^j_i - y^{j-1}_i \vert \over\vert y^j_i\vert}.\end{displaymath}$

After an index k is fixed, a suitable parameter value $\eta$ must be determined. A value of $\eta$ depends on the index k, on the location of the current solution on the branch (i.e., on j), and on the desired step size $\sigma$ ,

$\begin{displaymath}\eta =\eta (k,j,\sigma).\end{displaymath}$

A simple strategy relates the new step size $\eta -y^j_k$ to the previous step size y^j_k -y^j-1_k by an adjustable factor $\xi$ ,

$\begin{displaymath}\eta = y^j_k + (y^j_k -y^{j-1}_k)\xi .\eqno (11)\end{displaymath}$

An example for the adjustable factor $\xi$ will be given in Section 5.

The local parameterization concept can be generalized to a continuation that involves qualitative aspects. For example, a continuation by asymmetry is furnished by

$\begin{displaymath}p({\bf y},\lambda,\gamma)=y_k - y_m -\gamma \quad (\gamma \ne 0).\end{displaymath}$

4. Correctors

In this section, we discuss how to solve Eq.(1) iteratively, starting from the predictor $\bar {\bf Y}$ , such that the prescribed parameter $\gamma$ is reached. The easiest method is to solve the extended system Eqs. (6) or (10). Because these systems are ready to be solved by the standard software SOLVER, this type of corrector needs not be discussed further. As an alternative, a parameterization can be established by imposing a side condition on the iteration method. To this end, consider one step of the Newton iteration, formulated for the (n+1)-dimensional vector ${\bf Y}=({\bf y},\lambda),$

$\begin{displaymath}{\bf f}_{\bf y}\Delta {\bf y}+ {\bf f}_\lambda \Delta \lambda= - {\bf f}({\bf y}^{(\nu)},\lambda^{(\nu)}), \end{displaymath}$

$\begin{displaymath}{\bf y}^{(\nu+1)} = {\bf y}^{(\nu)} + \Delta {\bf y}, \ \ \lambda^{(\nu+1)} = \lambda^{(\nu)} +\Delta \lambda.\end{displaymath}$

In this system of n equations in n+1 unknowns $\Delta {\bf y}, \Delta \lambda$ , the first-order partial derivatives are evaluated at $({\bf y}^{(\nu)}$ , $\lambda^{(\nu)})$ . The system can be completed by attaching one further equation that parameterizes the course of the corrector iteration. For example, one requests that the iteration be perpendicular to the tangent ${\bf z}$ . Using the (n+1) scalar product, this is written as

$\begin{displaymath}( \Delta {\bf y}\hbox{{$^t$}\hbox to 3.0pt{\hss $^r$}}, \Delta \lambda ){\bf z}= 0\end{displaymath}$

which completes the iteration algorithm. Starting from the predictor, $({\bf y}^{(0)} ,\lambda^{(0)}): = (\bar {\bf y}^{j+1},\bar \lambda_{j+1} )$ , this iteration defines a sequence of corrector iterations ${\bf Y}^{(\nu)}$

$\begin{displaymath}({\bf y}^{(\nu)},\lambda^{(\nu)}), \ \ \nu =1,2,\ldots . \end{displaymath}$

This sequence eventually hits the branch in the solution that is the intersection of the curve defined by ${\bf f}({\bf y},\lambda )=\00$ and the hyperplane defined by the orthogonality to ${\bf z}$ . In the parameterizing equation, the tangent vector ${\bf z}$ can be replaced by other vectors.

Conceptual differences among various parameterizations are not significant. In a practical implementation, however, differences become substantial. Equations (6) and (10) can be solved without requiring specific software. Alternatively, the block structure can be exploited; available decompositions of ${\bf f}_{\bf y}$ can be used for the decomposition of ${\bf F}_{\bf Y}$ .

5. Step controls

In simple problems the principles introduced above may work effectively without a step-length control. That is, constant step lengths are taken throughout. If the step size is small enough, such a step strategy may be successful for a wide range of problems. But such results are often obtained in an inefficient manner, involving too many steps along ``flat" branches. The step length should be adapted to the actual convergence behavior. Because step controls must meet the features of the underlying combination predictor/parameterization/corrector, step-length algorithms are specifically designed.

Step controls can be based on estimates of the convergence quality of the corrector iteration. Such methods require a kind of absolute convergence measure to decide what is ``fast," or ``slow." A basic criterion for scaling step-length algorithms can be based on the observation that the total amount of work involved in a continuation depends on the average step length in a somewhat convex manner: The continuation is expensive both for very short steps (too many steps) and for very large steps (slow or no convergence of correctors). The costs of a continuation are moderate for a certain medium step length, which is related to an optimal number $N_{\rm opt}$ of iterations of a corrector. This number depends on the type of corrector and on the prescribed error tolerance $\epsilon$ . For example, with quasi-Newton correctors and $\epsilon =10^{-4}$ the optimal number is $N_{\rm opt}\approx 6.$ The aim is to adjust the step size so that each continuation step needs about $N_{\rm opt}$ corrector iterations. Let N_j denote the number of iterations needed to approximate the previous continuation step. Then a simple strategy is to reduce the step size in case $N_j > N_{\rm opt}$ and to increase the step size in case $N_j < N_{\rm opt}$ . This can be done, for example, by updating the previous step size by multiplication with the factor

$\begin{displaymath}\xi = N_{\rm opt} / N_j ;\end{displaymath}$

compare Eq.(11). In case of local parameterization, this leads to the value

$\begin{displaymath}\eta :=y^j_k +(y^j_k - y^{j-1}_k) N_{\rm opt}/N_j \end{displaymath}$

to be prescribed in Eq.(10) for the current parameter y_k. This step control is easy to implement. Further limitations of the step lengths may be advisable in order to obtain enough information about the branch. A strategy that is easy to implement is to limit relative changes $\Vert\hbox{predictor}\Vert / \Vert{\bf Y}\Vert$ to a value not larger than, say, 0.1. In this way small details of branches most likely are resolved.

6. Historical and bibliographical remarks on continuation

We conclude the section by adding some notes about the development of the continuation subject. In the 1960s, early papers suggesting basic ideas were [Haselgrove, 1961], [Klopfenstein, 1961], [Deist & Sefor, 1967]. One special aspect of continuation is homotopy, a strategy to facilitate the solution of a ``difficult" problem ${\bf g}({\bf y})=\00$ . The homotopy procedure is a way to set up a chain of intermediate equations with increasing difficulty such that the first equation is easy to solve, and the last equation is ${\bf g}({\bf y})=\00$ . Introducing a ``difficulty parameter" $\delta$ , and denoting the easy problem ${\bf\bar g}({\bf y})=\00$ , a systematic procedure to set up a homotopy is to solve

$\begin{displaymath}{\bf f}({\bf y},\delta):=\delta{\bf g}({\bf y})+(1-\delta){\bf\bar g}({\bf y})=\00,\end{displaymath}$

starting from $\delta=0$ , and ending at $\delta=1$ . That is, homotopy is an application of continuation. Several early papers were dedicated to the homotopy aspect.

In the 1970s, the interest shifted towards more algorithmic issues such as step length control, and to the calculation of general branches. Basic methods have been explained in this tutorial. Pseudo arclength was advocated by [Riks, 1972], [Keller, 1977], and local parameterization by [Rheinboldt, 1980], [Seydel, 1979b], [Seydel, 1984]. The updating of step lengths by orientation on an optimal number of steps $N_{\rm opt}$ was suggested in [Seydel, 1977], [Seydel, 1984]. Such a strategy has become a core of many step length algorithms. It has turned out that simple continuation principles work well on most problems. For specific methods on continuation see [Menzel & Schwetlick, 1978], [Den Heijer & Rheinboldt, 1981], [Rheinboldt & Burkardt, 1983], [Deuflhard et al., 1987]; further references can be found in [Seydel, 1994]. Technical issues of continuation are discussed in [Rheinboldt et al., 1990]. An account of simplicial methods is included in [Allgower & Georg, 1990].

References

Allgower, E.L. & Georg, K. [1990] Numerical Continuation Methods (Springer, Berlin).

Deist, F.H. & Sefor, L. [1967] ``Solution of systems of non-linear equations by parameter variation," Computer J. 10, 78-82.

Den Heijer, C. & Rheinboldt, W.C. [1981] ``On steplength algorithms for a class of continuation methods," SIAM J. Numer. Anal. 18, 925-948.

Deuflhard, P., Fiedler , B. & Kunkel, P. [1987] ``Efficient numerical path following beyond critical points," SIAM J. Numer. Anal. 24, 912-927.

Haselgrove, C.B. [1961] ``The solution of nonlinear equations and of differential equations with two-point boundary conditions," Comput. J. 4, 255-259.

Keller, H.B. [1977] `` Numerical solution of bifurcation and nonlinear eigenvalue problems," in Applications of Bifurcation Theory, ed. Rabinowitz, P.H. (Academic Press, New York).

Klopfenstein, R.W. [1961] `` Zeros of nonlinear functions," J. ACM 8, 366-373.

Menzel, R. & Schwetlick, H. [1978] ``Zur Lösung parameterabhängiger nichtlinearer Gleichungen mit singulären Jacobi-Matrizen," Numer. Math. 30, 65-79.

Rheinboldt, W.C. [1980] ``Solution fields of nonlinear equations and continuation methods," SIAM J. Numer. Anal. 17, 221-237.

Rheinboldt, W.C. & v. Burkardt, J. [1983] ``A locally parametrized continuation process," ACM Trans. of Math. Software 9, 215-235.

Rheinboldt, W.C., Roose, D. & Seydel, R. [1990] ``Aspects of continuation software," in Continuation and Bifurcations: Numerical Techniques and Applications, eds. Roose, D. et al. (Kluwer Academics Publisher) 261-268.

Riks, E. [1972] ``The application of Newton's method to the problem of elastic stability," Trans. ASME, J. Appl. Mech. 1060-1065.

Seydel, R. [1977] ``Numerische Berechnung von Verzweigungen bei gewöhnlichen Differentialgleichungen," Ph.D. thesis. Report TUM 7736, Mathem. Institut, Technical Univ. Munich.

Seydel, R. [1979b] ``Numerical computation of primary bifurcation points in ordinary differential equations," in Constructive Methods for Nonlinear Boundary Value Problems and Nonlinear Oscillations. Proceedings of a Conference in Oberwolfach 1978, eds. Albrecht, J., Collatz, L. & Kirchgässner, K. (Birkhäuser, Basel) ISNM 48, 161-169.

Seydel, R. [1984] ``A continuation algorithm with step control," in Numerical Methods for Bifurcation Problems. Proceedings of a Conference in Dortmund, 1983, eds. Küpper, T., Mittelmann, H.D. & Weber, H. (Birkhäuser, Basel) ISNM 70, 480-494.

Seydel, R. [1994] Practical Bifurcation and Stability Analysis. From Equilibrium to Chaos. Second Edition. Springer Interdisciplinary Applied Mathematics, Vol. 5. (Springer, New York).

Postscript-File for better printing results:

This Tutorial